[그림1]
일반적인 소리의 파형

---

[그림2]
아날로그 형태의 파형을
디지털 형태로 변환

---

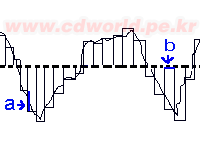
[그림3]
간격을 줄일수록 원래
아날로그 신호와 가깝게 된다

   소리는 공기를 통해 귀에 들려온다. 우리는 귀에는 [그림1]과 같은 파형의 소리가 전달된다. [그림1]에서 보는 바와 같이 각 파형은 진폭과 주파수를 갖는다. 진폭이 클수록 소리의 크기가 크다는 뜻으로 음량이 높다는 것을 나타낸다. 또한 주기가 짧을수록 일정 시간에 울리는 파형수가 많음을, 그리고 이런 소리는 음 높이가 높다는 것을 의미한다. 이 소리의 진동이 우리 귀의 고막을 진동시켜 결국 알아 듣게 되는 것이다.

   한편 소리는 디지털값이 아닌 아날로그값이다. 모든 소리값은 계속적으로 연속되어 변한다.우리 귀는 굉장히 빨리 변하거나 미세한 변화는 거의 느끼지 못하며, 컴퓨터 역시 아날로그 값을 기억할 수 없으므로 디지털 값으로 변환이 필요하다. 따라서 [그림1]의 파형을 [그림2]와 같이 논리적으로 변화시킨다고 가정할 때, 우리의 귀는 거의 느끼지 못해 원래 소리와 같다고 느끼게 된다. 이런점을 이용해 컴퓨터에서는 모든 아날로그 형태의 소리를 [그림2]의 파형과 같이 변화시킨다. 이때 사용하는 기계가 바로 ADC (Analog to Digital Converter)이다. 이 기계는 아주 짧은 일정시간마다 그때의 아날로그값을 측정하여 디지털 값으로 변환시켜 저장하게 된다.

    ADC로 소리는 변화시킬 경우 2가지 미리 생각해 볼 변수가 있다. [그림3]에서 ⓐ와 ⓑ의 간격이 클수록 변화된 소리는 원래 아날로그 신호와 거리가 멀게된다. 따라서 이런 간격을 줄일수록 변화된 신호는 원래의 아날로그 신호와 가깝게 된다. 먼저 ⓐ를 줄이기 위해서는 변화시킬 아날로그값을 보다 세밀하게 디지털값으로 변화시키면 된다. 예를 들어 한 번 측정해 디지털값으로 변환할 때 1byte로 하느냐 2byte로 하느냐, 아니면 더 많은 byte를 사용하느냐에 따라 변환된 값은 보다 높은 해상도를 갖게된다. 2byte를 사용할 경우 1byte를 사용했을때보다 2배의 메모리가 필요하지만 실제 연주되는 소리의 질은 2byte를 사용할 경우가 1byte를 사용했을때보다 약 256배 정도의 높은 해상도를 가지므로 논리적으로 256배 정도 더 좋은 음질의 소리를 낼 수 있다고 할 수 있다.

ⓑ를 줄이기 위해서는 일정 시간에 나타나는 디지털값들이 보다 많도록 하는 것이다.
그러기 위해서는 일정 시간동안 보다 많은 변환을 하면 된다.
이 때 알아야 할 것이 샘플링 주파수이다.